Derivation of the MFSK algorithm used in automotive radar systems

This article describes the derivation of MFSK algorithm, which provides the possibility to detect the range and velocity of multiple targets in automotive radar systems.

Considering the waveform of MFSK as depicted,

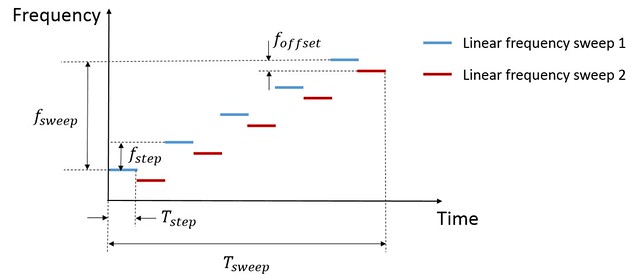
[This picture is copied from Matlab doc]

Here, there are $2N$ steps in the waveform. $f_{sweep} = (N-1) f_{step}$ is the frequency sweep range. $f_{step}$ is the frequency shift between ajacent steps in sweep 1 or sweep 2 sequence. $f_{offset}$ is the frequency offset between sweep 1 and sweep 2. $T_{chirp} = 2N T_{step}$ is the chirp time duration. $T_{step}$ is the time of single step.

Assume the range from radar to target is $R$ and the relative velocity of target to radar is $v$. The beat frequency which is the frequency difference as the receive signal is down-converted by the instantaneous transmitted signal can be expressed as follows.

\begin{equation} \label{eq_fb_raw} f_b = -\left( \frac{f_{sweep}}{T_{chirp}} T_{delay} - f_d \right) = \frac{2v}{\lambda} - \frac{f_{sweep}}{T_{chirp}} \frac{2R}{c} \end{equation}

\begin{equation} \frac{\Delta \phi}{2 \pi} = - \left( f_{offset} T_{delay} - f_d T_{step} \right) = \frac{2v}{\lambda} T_{step} - f_{offset} \frac{2R}{c} \end{equation}

where $T_{delay} = 2R / c$ is the time delay of echoes and $f_d = 2v / \lambda$ stands for the Doppler frequency shift. The $v$ is positive when the target is approaching radar.

Define $\bar{f_b} = f_b T_{chirp}$, $\Delta \bar{\phi} = \Delta \phi / (2\pi)$, $\bar{v} = v / \Delta v$, $\bar{R} = R / \Delta R$, $\bar{T}_{step} = T_{step} / T_{chirp}$, $\bar{f}_{offset} = f_{offset} / f_{sweep}$,

$$ \Delta R = \frac{c}{2 f_{sweep}} $$

and

$$ \Delta v = \frac{\lambda}{2 T_{chirp}} $$

The equations above can be normalized as following.

\begin{equation} \label{eq_fb} \bar{f_b} = \bar{v} - \bar{R} \end{equation}

\begin{equation} \label{eq_dphi} \Delta \bar{\phi} = \bar{T}_{step} \bar{v} - \bar{f}_{offset} \bar{R} \end{equation}

The $R$ and $v$ will be easily solved from eqs (\ref{eq_fb}) and (\ref{eq_dphi}).

\begin{equation} \label{eq_R} \bar{R} = ( \bar{T}_{step} - \bar{f}_{offset} )^{-1} ( \Delta \bar{\phi} - \bar{T}_{step} \bar{f}_b ) \end{equation}

\begin{equation} \label{eq_v} \bar{v} = ( \bar{T}_{step} - \bar{f}_{offset} )^{-1} ( \Delta \bar{\phi} - \bar{f}_{offset} \bar{f}_b )\end{equation}

In case we choose $f_{offset} = - \frac{1}{2} f_{step} = - \frac{f_{sweep}}{2(N-1)}$, the eqs (\ref{eq_R}) and (\ref{eq_v}) can be further written as following.

\begin{equation} \label{eq_simple_R} \bar{R} = \frac{2N(N - 1)}{2N - 1} \Delta \bar{\phi} - \frac{N - 1}{2N - 1} \bar{f_b} \simeq (N - 1) \Delta \bar{\phi} - \frac{\bar{f_b}}{2} \end{equation}

\begin{equation} \label{eq_simple_v} \bar{v} = \frac{2N(N - 1)}{2N - 1} \Delta \bar{\phi} + \frac{N}{2N - 1} \bar{f_b} \simeq (N - 1) \Delta \bar{\phi} + \frac{\bar{f_b}}{2} \end{equation}

From eqs (\ref{eq_simple_R}) and (\ref{eq_simple_v}), we know the roles of $\Delta R$ and $\Delta v$ are the range resolution and velocity resolution, respectively.

References

[1] Rohling, H. and M. Meinecke. Waveform Design Principle for Automotive Radar Systems, Proceedings of CIE International Conference on Radar, 2001.

[2] Simultaneous Range and Speed Estimation Using MFSK Waveform from Matlab documents.

Comments

Derivation of the MFSK algorithm used in automotive radar systems

Published

Category

Tags